Gito matematika susah ga?: Kalkulus Integral

integral adalah bentuk operasi matematika yang menjadi invers (kebalikan) dari sebuah operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu.

Berdasarkan pengertian diatas, ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral. Yakni:

Yang Pertama yaitu: Integral sebagai invers atau kebalikan dari turunan yang disebut sebagai Integral Tak Tentu. Yang Kedua yaitu: Integral sebagai limit dari jumlah atau suatu luas daerah tertentu yang disebut Integral Tentu.

Integral Tak Tentu

Integral tak tentu ini dari suatu fungsi dinotasikan sebagai berikut:

$\int f(x) dx$

Pada notasi tersebut, dapat dibaca sebagai integral terhadap notasi x yang disebut integran.

Secara umum integral dari fungsi f(x) ialah penjumlahan F(x) dengan C atau ditulis:

$\int f(x) dx = F(x)$

Oleh karena integral dan turunan saling berkaitan, maka rumus integral dapat diperoleh dari rumusan penurunan tersebut. Maka turunan ialah:

$\frac{d}{dx}\frac{a}{(n+1)}x^{(n+1)} = ax^n$

Maka rumus integral aljabar akan diperoleh:

$\int ax^n dx = \frac{a}{(n+1)}x^{n+1} + C$

dengan syarat-syarat 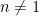$n \neq 1$ .

Sebagai bahan contoh, lihatlah integral aljabar fungsi-fungsi berikut:

$\int 4x^3dx=\frac{4}{(3+1)}x^{(3+1)}+ C = x^4 + C$
$\int \frac{1}{x^3}dx = \int x^{-3} dx = \frac{1}{(-3+1)}x^{-3+1}+C$
$= -\frac{1}{2}x^{-2}+C = -\frac{1}{2x^2}+C$
$\int 4x^3 - 3x^2 dx = \frac{4}{(3+1)} x^{(3+1)} + \frac{3}{(2+1)}x^{(2+1)}+C$
$= x^4+x^3+C$