Gito matematika susah ga?: Integral Substitusi

Teknik Integral Substitusi Dalam Fungsi Aljabar

Pada teknik ini, bentuk fungsi f(x) dapat diubah menjadi bentuk 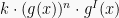$k \cdot (g(x))^n \cdot g^I(x)$ . Perhatikan bahwa jika U = g(x), maka $\frac{dU}{dx}g^I(x)$ atau $dU = g^I(x)\, dx$ .

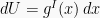Maka, integral ini dapat diselesaikan dengan memisalkan U = g(x) dan $U = g^I(x)dx$ sehingga diperoleh persamaan:

$\int f(x)\, dx = k \cdot \int(g(x))^n \cdot g^I(x)dx=k \cdot \int(U)^n \cdot dU$

$= \frac{k}{n+1}U^{(n+1)}+C$

untuk $n \neq -1$ .

Jika saja $n = -1$ , maka:

$k \cdot \int(U)^{-1} \cdot dU = \ln U+C$ .

contoh:

Jika 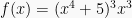$f(x)=(x^4+5)^3 x^3$ , untuk mendapat integralnya dengan memisalkan:

$x^4+5 = U$ dan $\frac{dU}{dx}=4x^3$

sehingga $x^3 dx=\frac{1}{4} dU$ .

Berdasarkan permisalan ini, maka persamaan integralnya menjadi:

$\int(x^4+5)^3x^3\, dx=\int(U)^3 \cdot \frac{1}{4} dU$

$=\frac{1}{16}U^4+C$

Jika hasil integral diatas disubstitusi dengan permisalan U di peroleh:

$\frac{1}{16}U^4+C=\frac{1}{16}(x^4+5)^4+C$

Contoh diatas merupakan teknik substitusi pada integral tak tentu. Pada integral tertentu yang memiliki nilai pada interval 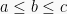$a \le b \le c$ tertentu, maka interval tersebut harus disubstitusi ke dalam interval baru untuk variabel U. Sebagai contoh jika 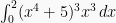$\int^2_0 (x^4+5)^3x^3\, dx$ , untuk mendapat integralnya dengan memisalkan: