- Menentukan gradien garis singgung suatu kurva
Gradien garis singgung (m) pada suatu kurva y = f(x) dirumuskan sebagai:
- Menentukan interval fungsi naik dan fungsi turun
Syarat interval fungsi naik 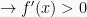
Syarat interval fungsi turun 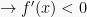
- Menentukan nilai stasioner suatu fungsi dan jenisnya
Jika fungsi y = f(x) kontinu dan diferensiabel di x = a dan f'(x) = 0, maka fungsi memiliki nilai statisioner di x = a. Jenis nilai stasioner dari fungsi y = f(x) dapat berupa nilai balik minimum, nilai balik maksimum, atau nilai belok. Jenis nilai stasioner ini bisa ditentukan dengan menggunakan turunan kedua dari fungsi tersebut.
- Nilai maksimum
 dan
dan 
Jika

dan
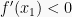
, maka
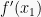
adalah nilai balik maksimum dari fungsi y = f(x) dan titik

adalah titik balik maksimum dari kurva y = f(x).
- Nilai minimum
 dan
dan 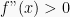
Jika

dan

, maka
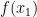
adalah nilai balik minimum dari fungsi

dan titik
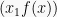
adalah titik balik minimum dari kurva y = f(x).
- Nilai belok
 dan
dan 
Jika

dan
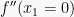
, maka
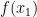
adalah nilai belok dari fungsi y = f(x) dan titik
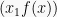
adalah titik belok dari kurva y = f(x).
- Menyelesaikan soal limit berbentuk tak tentu
 atau
atau 
Jika
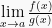
merupakan limit berbentuk tak tentu

atau

, maka penyelesaiannya dapat menggunakan turunan, yaitu f(x) dan g(x) masing-masing diturunkan.
Jika dengan turunan pertama sudah dihasilkan bentuk tertentu, maka bentuk tertentu itu adalah penyelesaiannya. Tetapi jika dengan turunan pertama masih dihasilkan bentuk tak tentu, maka masing-masing f(x) dan f(x) diturunkan lagi sampai diperoleh hasil berbentuk tertentu. Cara penyelesaian seperti ini disebut Dalil L’hopital.
- Menentukan rumus kecepatan dan percepatan
Jika rumus atau persamaan posisi gerak suatu benda sebagai fungsi waktu diketahui yaitu s = f(t), maka rumus kecepatan dan kecepatannya dapat ditentukan yaitu:
- Rumus kecepatan
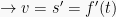
- Rumus percepatan

Tidak ada komentar:
Posting Komentar