Menyelesaikan soal limit berbentuk tak tentu

Jika 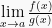 merupakan limit berbentuk tak tentu   atau , maka penyelesaiannya dapat menggunakan turunan, yaitu f(x) dan g(x) masing-masing diturunkan.

Jika dengan turunan pertama sudah dihasilkan bentuk tertentu, maka bentuk tertentu itu adalah penyelesaiannya. Tetapi jika dengan turunan pertama masih dihasilkan bentuk tak tentu, maka masing-masing f(x) dan f(x) diturunkan lagi sampai diperoleh hasil berbentuk tertentu. Cara penyelesaian seperti ini disebut Dalil L’hopital.

Contoh soal :

Hitunglah nilai limit fungsi aljabar berikut ini:

limx→2

 x² - 4x - 2

Pembahasan :
Jika hasil substitusi adalah 0/0 (bentuk tak tentu), maka tidak dapat dilakukan dengan cara memasukkan nilai langsung, melainkan harus difaktorkan terlebih dahulu

limx→2

 x² - 4x - 2 = 2² - 42 - 2 = 00 (bentuk tak tentu)

Jadi hasil faktornya adalah :

limx→2

 x² - 4x - 2 = (x-2)(x+2)(x-2) = (x+2)= (2+2) = 4

2. Hitunglah nilai limit fungsi aljabar berikut ini:

limx→2

 x² - 5x + 6x² - 4

Pembahsan :

Jika disubstitusi langsung, maka akan didapatkan :

limx→2

 x² - 5x + 6x² - 4 = 2² - 5.(2) + 62² - 4 = 00 (bentuk tidak tentu)

Dengan demikian kita harus menggunakan cara lain, yaitu : dengan mengfaktorkan dan melakukan turunan. Dalam soal no.4 ini kita lakukan dengan turunan :

limx→2

 x² - 5x + 6x² - 4 = 2x - 52x = 2.(2) - 52.(2) = -14